Как узнать, является ли бинарное дерево ( поиска ) строгим

На своем курсе «Алгоритмы и структуры данных» я показываю студентам, как проверить двоичное дерево ( поиска ) на строгость. Поэтому решил написать эту статью-шпаргалку.

➡ Во-первых, на строгость можно проверять не только поисковое двоичное дерево, а просто бинарное дерево. Поэтому во всех выкладках буду оперировать простым двоичным деревом.

➡ Во-вторых, нужно понимать, что любая вершина двоичного дерева имеет степень.

Степенью вершины бинарного дерева называют количество ее потомков. Очевидно, что максимальная степень узла бинарного дерева составляет $2$, когда узел имеет обоих сыновей.

В одной из своих заметок я показывал ( в том числе и программным кодом ), как программно определить статус вершины. По факту статус вершины выражается количеством ее потомков.

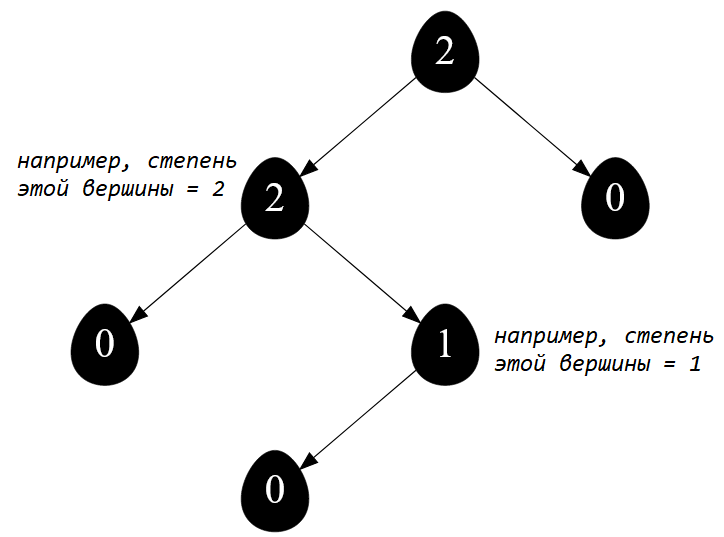
Рисунок — ключами узлов выступает их степень ( количество потомков )

➡ В-третьих, и это самое важное, нужно знать, что в теории структур данных понимают под строгим двоичным деревом:

Двоичное дерево называется строгим, если все его вершины имеют степень $0$ или $2$. Другими словами, каждый узел дерева имеет либо $2$ потомка, либо ни одного.

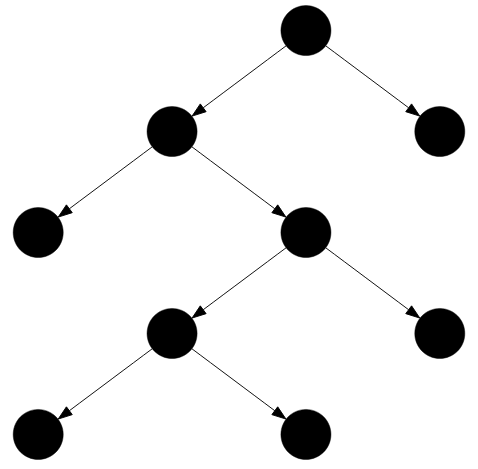
Рисунок — строго двоичное дерево ( поиска )

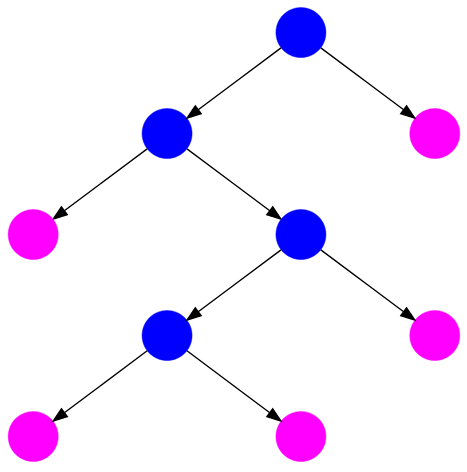
Рисунок — строго бинарное дерево ( поиска ), у которого синие узлы имеют степень $2$, а бордовые — степень $0$

➡ Соответственно, главный вопрос: как узнать, что «перед тобой» строго двоичное дерево? То есть на вход подается произвольное бинарное дерево и требуется проверить его на строгость.

💡 Лично бы я посчитал количество неполных узлов в данном дереве. Если бы это количество оказалось равным $0$, то автоматически бы это означало, что все вершины дерева имеют либо степень $2$, либо степень $0$, что соответствует строгому двоичному дереву ( поиска ).

Пишите в комментариях, что непонятно по алгоритму проверки произвольного двоичного дерева на строгость. Также напишите, при каких обстоятельствах вам приходилось взаимодействовать со строго бинарным деревом.