В любой программе, где было задействовано двоичное дерево ( поиска ), при ее завершении обязательно нужно высвобождать динамическую память.
Другими словами, при завершении работы программы нужно удалять все узлы двоичного дерева ( поиска ).
Алгоритм, который я хочу рассмотреть в этой статье-шпаргалке, не зависит от того, является ли дерево поисковым или просто бинарным деревом. Поэтому во всех примерах я буду рассматривать анонимные двоичные деревья.

Рисунок — стандартное анонимное бинарное дерево ( поиска )
➡ В одной из своих статей я показывал, как удалить заданный узел из двоичного дерева поиска. Теоретически этот алгоритм можно применить для того, чтобы удалить все узлы дерева. Но это будет крайне не оптимально из-за накладных расходов, связанных с определением статуса удаляемой вершины, поиска минимального элемента в правом поддереве и т.д.
💡 Гораздо удобнее «уничтожить» все вершины дерева, используя один из обходов дерева.
Всего существует $6$ базовых обходов бинарного дерева:
| # | Официальное название | Мое название |
| $1$ | Прямой левый | KLP |
| $2$ | Прямой правый | KPL |
| $3$ | Обратный левый | LPK |
| $4$ | Обратный правый | PLK |
| $5$ |
Симметричный левый |
LKP |
| $6$ | Симметричный правый | PKL |
➡ Но не каждый обход пригоден для последовательного удаления всех узлов заданного двоичного дерева.
Кстати, почему я говорю про обход дерева, когда нужно удаление вершин дерева? Дело в том, что при обходах посещается каждая вершина бинарного дерева и с ней можно производить любые операции. В этом алгоритме ее нужно удалять.
Например, я рассмотрю прямой левый обход ( KLP ). Сначала посещается сам узел, затем рекурсивный спуск в левое поддерево, а затем в правое поддерево. Допустим, нужно удалить первый обрабатываемый узел при таком «обходе» — это будет корень заданного двоичного дерева ( поиска ).
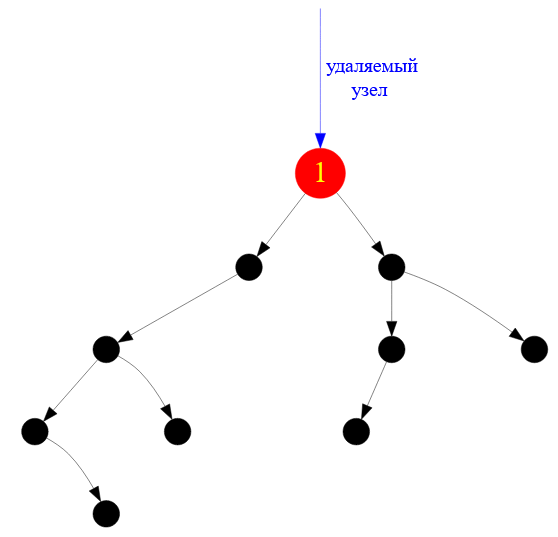
Рисунок — при KLP—обходе сразу нужно удалять корень дерева
Представим, что этот узел ( с меткой $1$ ) удален. В результате дерево становится разорванным на две половины: левое и правое поддерево:
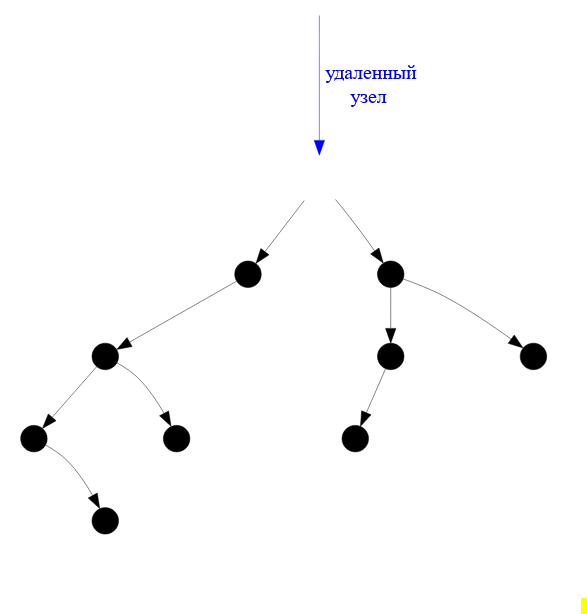
Рисунок — разорванное двоичное дерево после удаления вершины
💡 Очень важно понимать такой момент, что после удаления вершины уже программно нельзя обратиться к ее указателям на левое и правое поддерево.
Резюме: если постараться, то, конечно, можно адаптировать такой обход дерева ( KLP ) для удаления всех узлов, но это все не очень удобно. Тем более есть другие способы обхода узлов двоичного дерева!
Лично я считаю, что гораздо удобнее удалять вершину, которая не имеет потомков, то есть является листом. Следовательно, сначала надо «спуститься» вглубь дерева до листьев и последовательно удалять их. Удаляя листы, их родители также становятся постепенно листьями. В итоге весь процесс сводится к постепенному удалению листовых вершин.
➡ Для такого типа обходов идеально подходит LPK-обход или PLK-обход. То есть рекурсивно спускаемся до нижнего уровня дерева и лишь после этого начинаем удалять элементы.
Сначала уничтожается следующий узел заданного двоичного дерева ( поиска ):
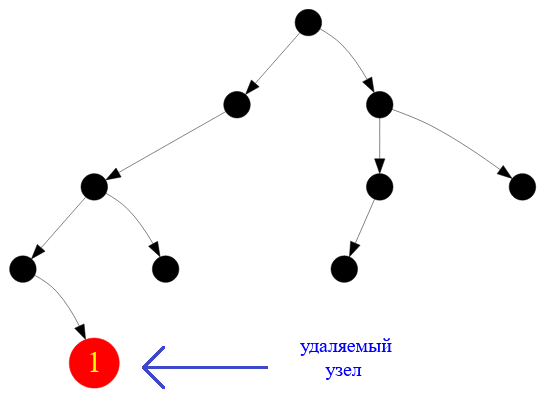
Рисунок — при LPK-обходе удаляется листовая вершина
Затем удаляем родительский узел ( с меткой $2$ ) относительно уже удаленного потомка ( с меткой $1$ ). Этот родительский узел, после удаления своего правого сына также стал листом.
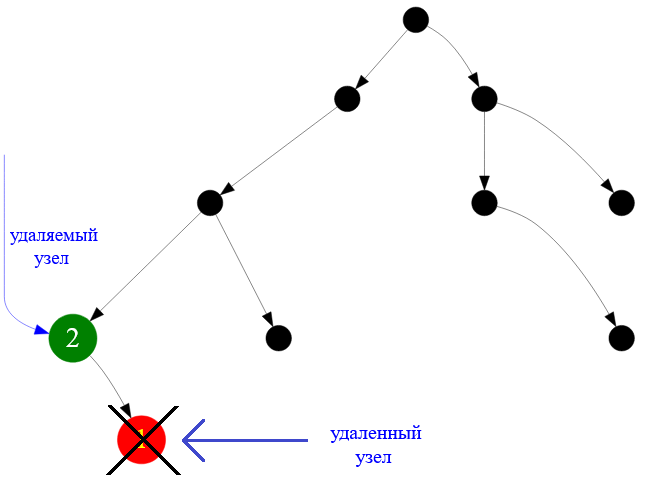
Рисунок — удаления узла, который в прошлом был родителем
Этот процесс продолжается до тех пор, пока не будет удалена корневая вершина заданного дерева. Именно эта вершина удаляется в последнюю очередь — это логично и максимально правильно!
➡ В этом алгоритме ( удаление бинарного дерева ) на полную катушку используется LPK-обход. А ведь этот обход посещения вершин двоичного дерева достаточно редко, когда нужен.
В результате я закодировал следующую функцию на языке Си, которая рекурсивно уничтожает все элементы заданного дерева ( поиска ):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
//------------------------------------------------------------------------------ // удаление всех узлов из дерева // node - указатель на обрабатываемый узел //------------------------------------------------------------------------------ void Clear_tree( Node* const node ) { // если вышли на NULL-указатель, то удаление физически невозможно if ( node != NULL ) { // сначала уходим в левое поддерево Clear_tree( node -> left ); // затем в правое поддерево Clear_tree( node -> right ); // удаляем текущую вершину, которая гарантировано является листовой free( node ); } } //------------------------------------------------------------------------------ |
➡ Есть такой нюанс: после завершения работы функции Clear_tree() указатель на корень удаленного дерева является висячим, ссылаясь на недопустимую ( высвобожденную ) память. Поэтому его следует отдельно занулить, например.
Пишите в комментариях, что непонятно в рамках рассмотренного алгоритма удаления двоичного дерева из памяти. Также подумайте, как можно адаптировать KLP-обход ( корень — левое поддерево — правое поддерево ) для удаления всех вершин дерева.
| ВНИМАНИЕ | Для заказа программы на двоичное дерево ( поиска ) пишите на мой электронный адрес proglabs@mail.ru |
Добавить комментарий