| ВНИМАНИЕ |
Для заказа программы на графовые алгоритмы любой сложности пишите на мой электронный адрес proglabs@mail.ru |
Как известно, гамильтонов цикл существует только в гамильтоновом графе. Поэтому встает вопрос: а как, собственно, узнать, что заданный неориентированный граф гамильтонов?
В этой статье-шпаргалке я покажу алгоритм, проверяющий заданный граф на «гамильтоновость». Этот алгоритм принято называть теоремой Дирака или условием Дирака.
Сама теорема Дирака звучит так:
Если в заданном неориентированном графе, состоящем из $n$ вершин ( $n \geq 3$ ), степень каждой вершины $deg( x ) \geq \frac{n}{2}$, то такой граф гамильтонов.
💡 Условие Дирака является достаточным условием существования гамильтонова цикла в графе.
💡 Неориентированный граф, который подчиняется теореме Дирака, иногда называют графом Дирака.
С точки зрения графовой символики условие Дирака можно записать так:
$deg( x )\ \geq\ \frac{n}{2}$, где
$x$ — любая из вершин графа;
$n$ — общее количество вершин графа;
$deg$ — обозначение степени вершины.
Очевидно, если $n$ — нечетное, например, $7$, то отношение $\frac{n}{2}$ будет не целым числом, например, для $n = 7$ это отношение составляет $3.5$. В таких случаях дробная часть отбрасывается ( происходит целочисленное деление ), то есть $\frac{7}{2} = 3$, а не $3.5$.
Покажу неориентированный невзвешенный граф, состоящий из $9$ вершин:
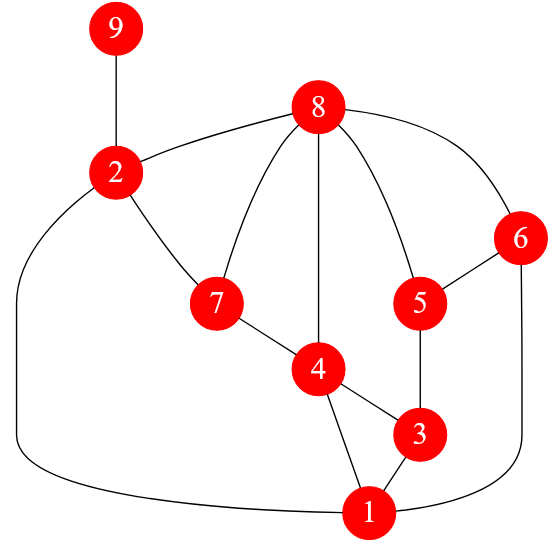
Рисунок — помеченный неориентированный невзвешенный граф, состоящий из $9$ вершин
➡ Интересно, а этот граф является гамильтоновым или все-таки нет?
Чтобы ответить на этот вопрос я буду действовать в соответствии с условием Дирака, то есть для начала определю степень каждой вершины графа.
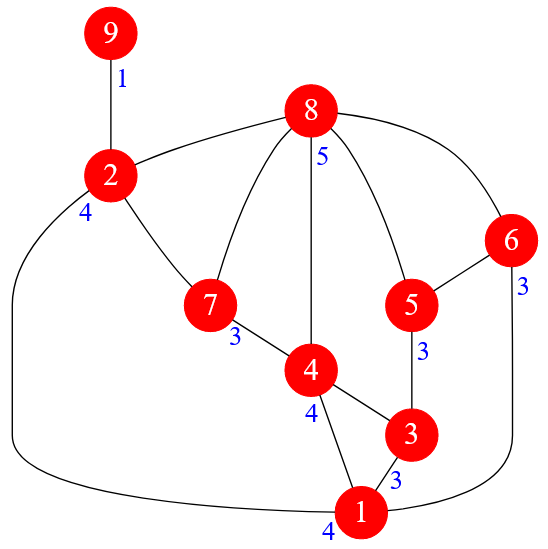
Рисунок — вершины графа с обозначением их степеней
Общее количество вершин в заданном графе: $n = 9$.
Теорема Дирака требует, чтобы степень любой вершины была не меньше половины общего количества вершин графа. Хочу рассмотреть, например, вершину с меткой $6$.
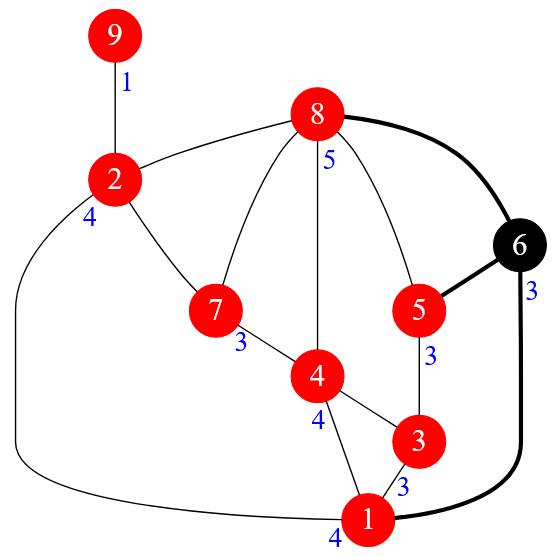
Рисунок — анализ вершины графа с меткой $6$
Степень вершины с меткой $6$ составляет $3$, то есть $deg( 6 ) = 3$. Наложим условие Дирака на эту вершину, то есть:
$deg( 6 ) \geq \frac{n}{2} \rightarrow 3 \geq \frac{9}{2} \rightarrow 3 \geq 4$ — false
Видно, что вершина $6$ не подчиняется правилу Дирака. Остальные вершины графа нет смысла проверять, так как условие Дирака «сломалось» при проверке одной из вершин графа.
💡 Чисто логически для себя делаю такой вывод: чтобы неориентированный граф был гамильтоновым, он должен обладать крайне высокой связностью, в идеале стремиться к полному графу.
Но стоит заметить, несмотря на то, что текущий граф не подчиняется теореме Дирака, это еще не означает, что он не гамильтонов. Это связано с тем, что условие Дирака является достаточным, а не необходимым.
Давайте проверим степени всех вершин ( их всего $9$ штук ) рассматриваемого графа на соответствие требованиям по Дираку:
| Метка вершины | Степень вершины | Соответствие по Дираку |
| $1$ | $4$ | $4 \geq \frac{9}{2},\ 4 \geq 4$ — true |
| $2$ | $4$ | $4 \geq \frac{9}{2},\ 4 \geq 4$ — true |
| $3$ | $3$ | $3 \geq \frac{9}{2},\ 3 \geq 4$ — false |
| $4$ | $4$ | $4 \geq \frac{9}{2},\ 4 \geq 4$ — true |
| $5$ | $3$ | $3 \geq \frac{9}{2},\ 3 \geq 4$ — false |
| $6$ | $3$ | $3 \geq \frac{9}{2},\ 3 \geq 4$ — false |
| $7$ | $3$ | $3 \geq \frac{9}{2},\ 3 \geq 4$ — false |
| $8$ | $5$ | $5 \geq \frac{9}{2},\ 5 \geq 4$ — true |
| $9$ | $1$ | $1 \geq \frac{9}{2},\ 1 \geq 4$ — false |
➡ В итоге $5$ вершин данного графа ( это вершины с метками $3,\ 5,\ 6,\ 7$ и $9$ ) не подчиняются условию Дирака.
Сейчас хочу поработать со следующим помеченным неориентированным графом и на него «наложить» условие Дирака:
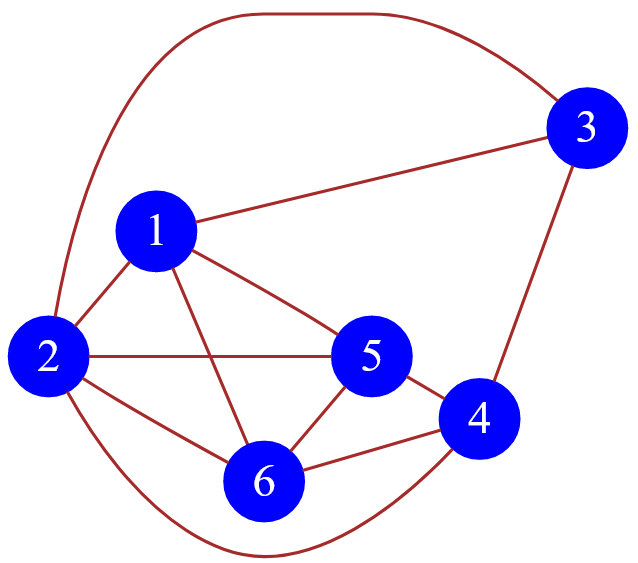
Рисунок — помеченный неориентированный граф, состоящий из $6$ вершин
Рассчитаю степень каждой вершины рассматриваемого графа. В итоге получаю такую картину:
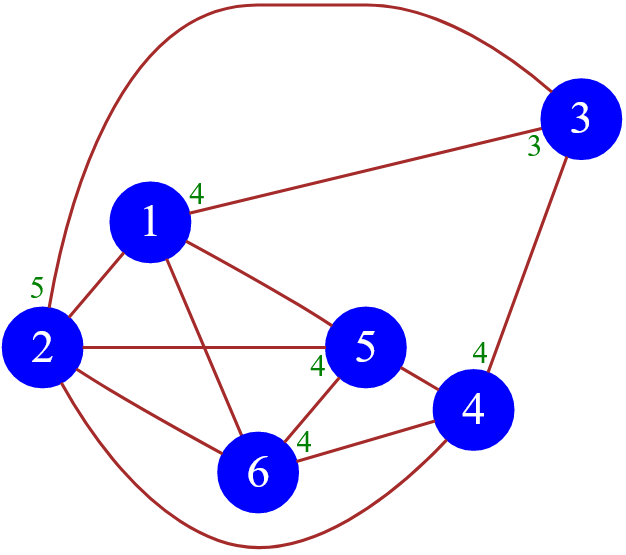
Рисунок — граф с обозначением степеней всех вершин ( зеленое число, стоящее рядом с вершиной )
Давайте проверим степени всех вершин ( их всего $6$ штук ) рассматриваемого графа на соответствие требованиям по Дираку:
| Метка вершины | Степень вершины | Соответствие по Дираку |
| $1$ | $4$ | $4 \geq \frac{6}{2},\ 4 \geq 3$ — true |
| $2$ | $5$ | $5 \geq \frac{6}{2},\ 5 \geq 3$ — true |
| $3$ | $3$ | $3 \geq \frac{6}{2},\ 3 \geq 3$ — true |
| $4$ | $4$ | $4 \geq \frac{6}{2},\ 4 \geq 3$ — true |
| $5$ | $4$ | $4 \geq \frac{6}{2},\ 4 \geq 3$ — true |
| $6$ | $4$ | $4 \geq \frac{6}{2},\ 4 \geq 3$ — true |
Во все случаях выполняется требование Дирака, следовательно, данный граф является гамильтоновым, то есть содержит как минимум один гамильтонов цикл.
Сейчас я визуально найду пару гамильтоновых циклов в текущем графе.
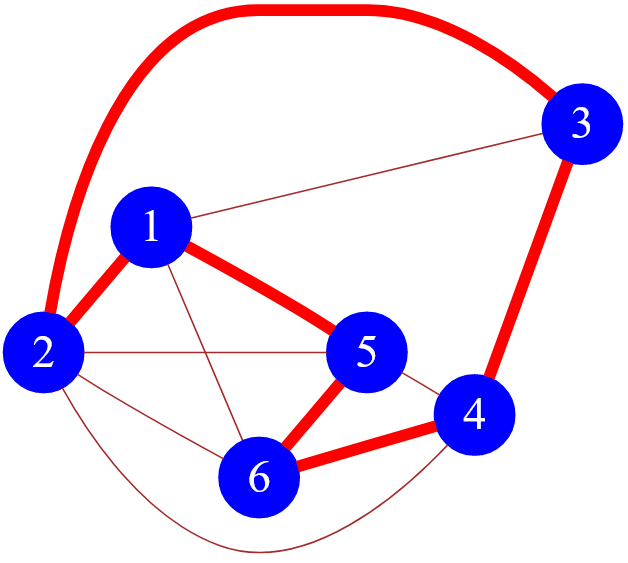
Рисунок — пример одного ( первого ) из множества гамильтоновых циклов ( $1\ -\ 2\ -\ 3\ -\ 4\ -\ 6\ -\ 5\ -\ 1$ )
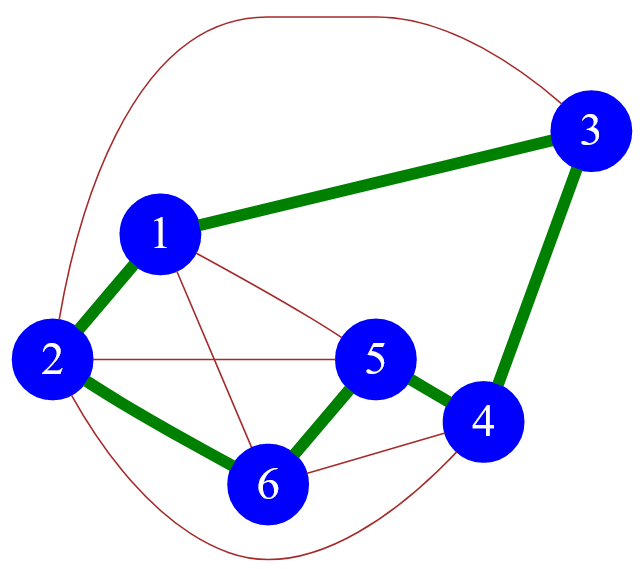
Рисунок — пример еще одного ( второго ) из множества гамильтоновых циклов ( $1\ -\ 3\ -\ 4\ -\ 5\ -\ 6\ -\ 2\ -\ 1$ )
➡ А сейчас хочу написать программу на языке Си, которая на вход принимает информацию о степенях вершин заданного неориентированного графа, и в качестве ответа сообщает мне, выполняется ли для этого графа теорема Дирака, то есть, является ли заданный граф гамильтоновым.
💡 В этой статье я показывал, как программно определить степени вершин в неориентированном графе, который задан матрицей смежности.
Полная информация о степенях всех вершин заданного неориентированного графа имеет вид:
| Метка вершины | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ |
| Степень вершины | $4$ | $5$ | $3$ | $4$ | $4$ | $4$ |
В результате у меня получилась следующая программа, которая, используя условие Дирака, проверяет заданный неориентированный граф на «гамильтоновость»:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
#include <stdio.h> // для ввода-вывода #include <stdlib.h> // служебные функции #include <locale.h> // русификация диалогов // количество вершин графа #define VERTEX_COUNT 6 //--------------------------------------------------------------------- // условие Дирака ( проверка графа на "гамильтоновость" ) // 0 - граф негамильтонов ( условие Дирака не выполняется ) // 1 - граф гамильтонов ( условие Дирака выполняется ) //--------------------------------------------------------------------- int Is_Dirak( const int degrees[] ) { int ivertex; // условие Дирака проверяется только на графах, состоящих не менее, чем из трех вершин if ( VERTEX_COUNT < 3 ) { return 0; } // просматриваем степени всех вершин графа for ( ivertex = 0; ivertex < VERTEX_COUNT; ivertex++ ) { // если для текущей вершины ее степень не соответствует правилу Дирака, то // прекращаем проверку ( остальные вершины можно уже не проверять ) if ( degrees[ ivertex ] < VERTEX_COUNT / 2 ) { return 0; } } // если степени всех вершин оказались не меньше половины общего // количечества вершин графа, значит, условие Дирака выполнилось return 1; } //--------------------------------------------------------------------- // главная функция программы ( точка входа ) //--------------------------------------------------------------------- int main( void ) { // хранит результат выполнения условия Дирака int is_Dirak; // массив хранит степени соответственных вершин const int degrees[ VERTEX_COUNT ] = { 4, 5, 3, 4, 4, 4 }; // русификация диалогов программы setlocale( LC_ALL, "Russian" ); // проверка заданного неориентированного графа на "гамильтоновость", накладывая на него условие Дирака is_Dirak = Is_Dirak( degrees ); if ( is_Dirak == 0 ) { printf( "Заданный граф не факт, что является гамильтоновым, так как не выполнилось условие Дирака." ); } else { printf( "Заданный граф на 100\%% является гамильтоновым, так как выполнилось условие Дирака." ); } // задержка работы программы, чтобы у пользователя была возможность просмотреть результат printf( "\n\n" ); return EXIT_SUCCESS; } |
А вот и результаты работы программы:

Рисунок — результаты работы программы
Очень важный момент: условие Дирака является достаточным, но не необходимым. Это означает, если заданный граф не подчиняется условию Дирака, то это еще не означает, что он не является гамильтоновым.
Вот вам пример неориентированного графа, для которого не выполняется теорема Дирака, но при этом он гамильтонов граф:
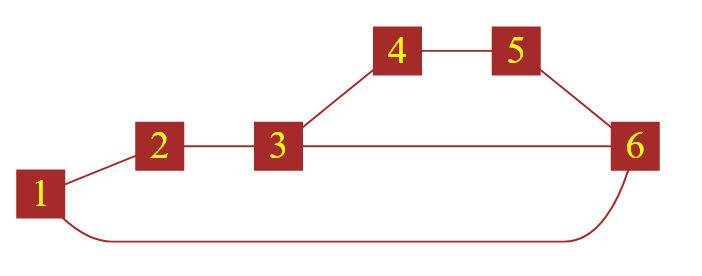
Рисунок — неориентированный граф, который не подчиняется условию Дирака
Доказать, что этот граф не соответствует требованиям Дирака элементарно. Рассмотрим вершину, например, с меткой $2$. Степень этой вершины равна $2$. Общее количество вершин графа равно $6$. Проверяем формульно условие Дирака:
$deg( 2 ) \geq \frac{6}{2} \rightarrow 2 \geq 3$ — false
➡ Условие Дирака не выполняется, но при этом рассматриваемый граф гамильтонов.
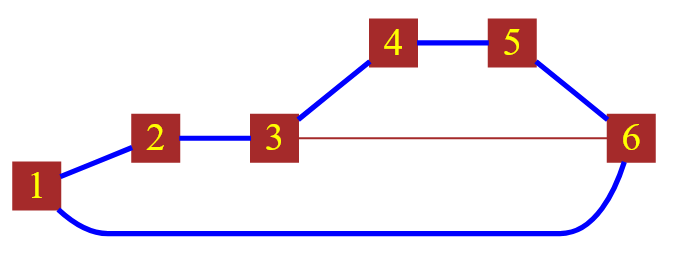
Рисунок — гамильтонов граф с показом гамильтонова цикла, который не подчиняется условию Дирака
Надо четко запомнить следующее: если граф подчиняется правилу Дирака, то он $100\%$ гамильтонов, но если граф гамильтонов, то не факт, что он подчиняется условию Дирака.
➡ Пишите в комментариях, что осталось непонятным в рамках рассмотренного алгоритма — наложения условия Дирака на неориентированный граф, для которого известны степени всех его вершин. Также расскажите, при каких обстоятельствах вам приходилось прибегать к теореме Дирака на практике.
Материал подготовил Александр Георгиевич, эксперт ЕГЭ по информатике, а также специалист по динамическим структурам данных и графовым алгоритмам: стеки, деки, очереди, списки, деревья, хеш-таблицы, графы и т.п. Для записи на частную подготовку или заказа работы по программированию звонить по номеру телефона: 8(926) 610 — 61 — 95 (электронный адрес: proglabs@mail.ru).
Добавить комментарий