Посмотрим на рис.1, на котором представлено классическое двоичное дерево поиска.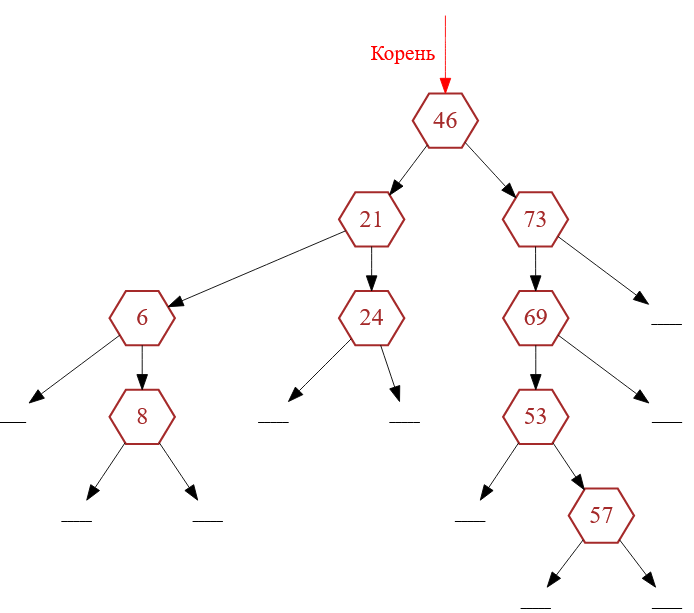
Рисунок 1 — Стандартное бинарное дерево поиска
Очевидно, что эту структуру неспроста называют двоичным деревом поиска. Ключевое слово здесь «поиска». Давайте рассмотрим конкретный узел данного дерева, например, узел с ключом равным $21$ (рис. 2).
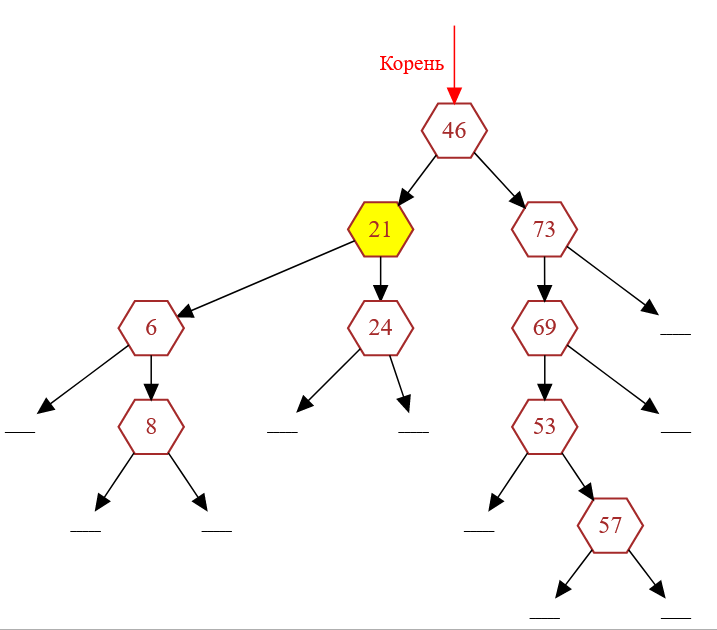
Рисунок 2 — Рассмотрение узла дерева с ключом равным $21$
Каждый узел двоичного дерева поиска имеет левое и правое поддерево, даже, если данные поддеревья являются пустыми. Узел с ключом $21$ имеет непустые левые и правые поддеревья. Все узлы, входящие в левое поддерево имеют значения ключей, меньшие, чем число $21$, а узлы, входящие в правое поддерево — большие, чем значение $21$.
➡ Сразу договоримся, что элементы, имеющие ключи-дубликаты, запрещены в поисковом дереве. То есть все вершины дерева имеют уникальные ключевые значения.
| Значения ключей для узла с ключом $21$ | Левое поддерево | Правое поддерево |
| $6,\ 8$ | $24$ |
➡ Следовательно, при добавлении очередного узла в бинарное дерево поиска, нужно будет учитывать следующее правило:
Если значение ключа добавляемого элемента меньше значения ключа текущей вершины, то движение происходит в левое поддерево, иначе — в правое поддерево. Непосредственно вставка происходит в момент, когда достигнуто свободное место в бинарном дереве.
Бинарное дерево поиска является рекурсивной структурой данных, поэтому в программах широко применяется их рекурсивная обработка. Но никто не запрещает обрабатывать «бинарки» итеративным способом — просто это гораздо менее удобно. Позже покажу оба варианта реализации: и рекурсивный, и итеративный.
💡 Благодаря упорядочиванию ключей особым образом в этой древовидной структуре поиск нужного узла (поиск проводится по ключу) осуществляется практически моментально, почти дихотомически (если дерево является сбалансированным).
Ранее мы объявили специальную переменную-указатель root, которая является указателем на вершину двоичного дерева поиска. Изначально дерево является пустым, то есть не содержит ни одного узла (рис. 3).
Рисунок 3 — Пустое двоичное дерево поиска (нет ни одного узла)
Когда происходит добавление самого 1-ого узла, то, очевидно, что этот добавляемый узел становится корнем дерева (рис. 4.). Допустим, происходит вставка узла с ключом равным $46$.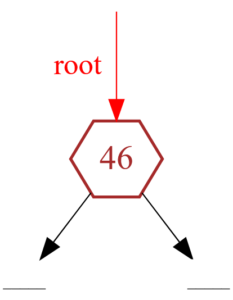
Рисунок 4 — Добавление 1-ого узла, который становится корнем дерева
Затем требуется добавить в двоичное дерево поиска узел с ключом равным $21$. Поиск позиции вставки всегда начинается с корня. То есть функция вставки элемента в дерево одним из параметров обязательно будет иметь указатель на его корень (понятно, что мы не рассматриваем ситуацию, когда переменная root является глобальной переменной, так как это нарушает почти все принципы правильного программирования).
➡ Иногда глобальные переменные действительно являются крайне полезными, но не в процессе обработки бинарного дерева поиска.
Так как ключ добавляемого элемента (это число $21$) меньше, чем ключевое значение корня (это число $46$), то движение по дереву уходит в левое поддерево. Так как левое поддерево является пустым, то это означает, что это место в дереве свободно и туда можно добавить новый узел (рис. 5).
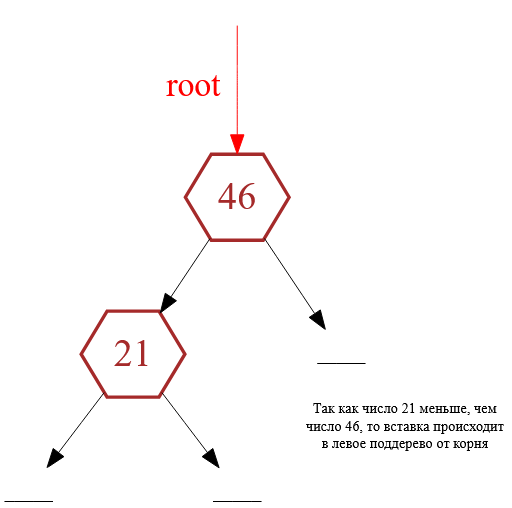Рисунок 5 — Добавление $2$-го узла с ключом равным $21$ ( вставка в левое поддерево от корня, так как $21 < 46$ )
Затем, например, делается попытка добавить узел с ключом равным $24$. Поиск позиции вставки всегда начинается с корня дерева с последующим погружением «внутрь» дерева. Так как $24 < 46$, то двигаемся в левое поддерево. Встречаем узел с ключом равным $21$. Так как $24 \geq 21$, то двигаемся в правое поддерево. А там пусто! Значит, мы нашли свободное место и помещаем туда $3$-ий элемент (рис. 6).
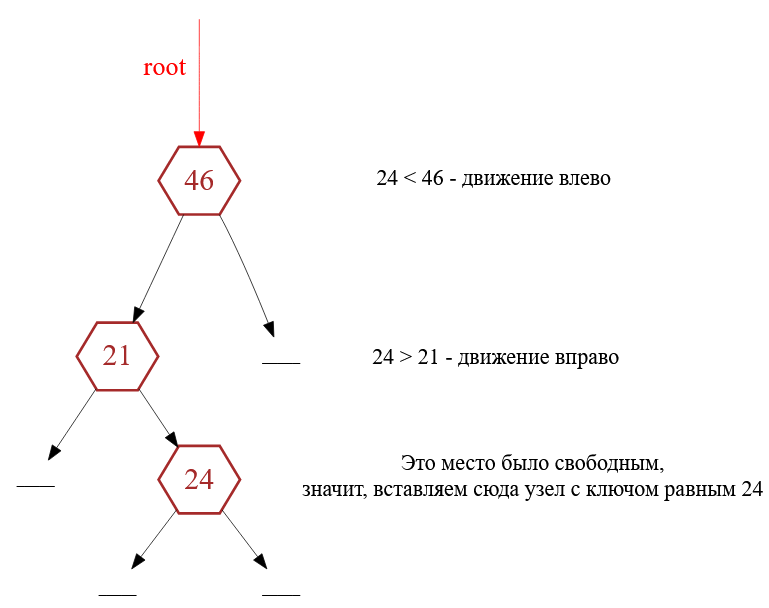Рисунок 6 — Добавление узла с ключом равным $24$
И давайте рассмотрим добавление еще одного узла, например, с ключом равным $73$. Как обычно поиск позиции вставки начинается с корня. Сравниваются ключи $73 \geq 46$, значит, двигаться нужно в правое поддерево. А там пусто ( NULL ), значит, позиция вставки найдена! (рис. 7).
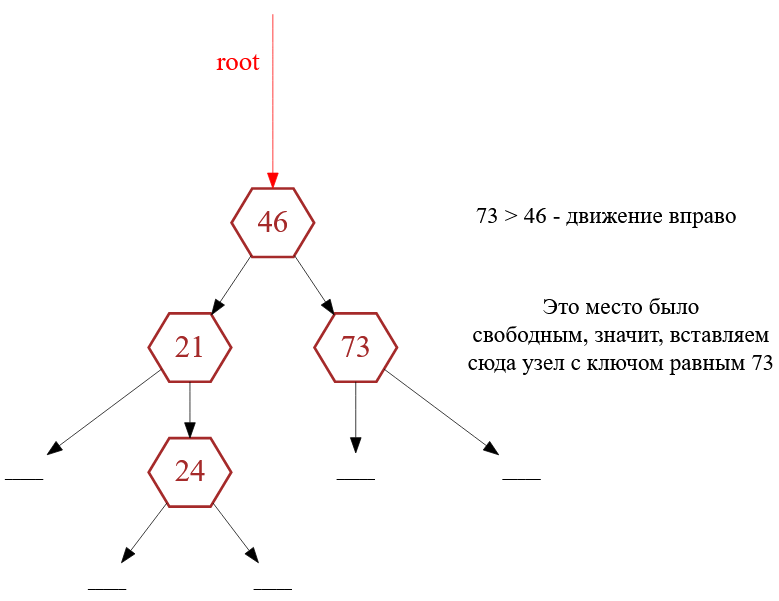
Рисунок 7 — Добавление узла с ключом равным $73$
И данный процесс можно продолжать бесконечно! Ну, почти бесконечно, так как все-таки объем оперативной памяти ограничен 🙂 . И наша задача все это дело закодировать рекурсией. То есть нам надо написать программную функцию вставки нового узла в бинарное дерево поиска.
Главное требование: после вставки дерево должно остаться в согласованном состоянии, то есть остаться двоичным деревом поиска!
➡ Какие входные параметры должна иметь эта программная функция добавления узла в «бинарку»? Очевидно, что потребуется:
- Указатель на корень дерева.
- Значение ключа вставляемого узла.
Указатель на корень дерева нужен, чтобы было от чего оттолкнуться в процессе движения по дереву. А значение ключа пригодится в процессе поиска свободной позиции в дереве, ведь движение в левое или в правое поддерево будет регулироваться именно значением ключа.
В итоге можно закодировать следующую рекурсивную функцию вставки:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
//------------------------------------------------------------------------------ // добавление новой вершины в двоичное дерево поиска ( дубликат не добавляется ) // root - указатель на корень дерева // key - ключевое значение добавляемой вершины // в качестве результата функция вернет указатель на вершину обновленного дерева //------------------------------------------------------------------------------ Node* Insert_node( Node* const root, const int key ) { if ( root == NULL ) { Node* new_node = Create_node( key ); return new_node; } // если в дереве уже есть вершина с таким же ключом if ( key == root -> key ) { return root; } if ( key < root -> key ) { root -> left = Insert_node( root -> left, key ); } else { root -> right = Insert_node( root -> right, key ); } return root; } //------------------------------------------------------------------------------ |
💡 Важнейший момент с точки зрения программирования заключается в том, что в качестве ответа возвращается указатель на корень дерева! Всегда!
Если этого не сделать, то будут большие проблемы при добавлении самого 1-ого элемента.
Также обратите внимание на эту проверку:
|
1 2 3 4 5 |
// если в дереве уже есть вершина с таким же ключом if ( key == root -> key ) { return root; } |
Это защита от дубликатов. Если делается попытка вставить узел с ключом, который уже присутствует в дереве, то просто выходим из рекурсивной функции.
Внимательный читатель обратит внимание на следующую строчку кода:
|
1 |
Node* new_node = Create_node( key ); |
Create_node — вспомогательная функция, которая занимается тем, что выделяет в памяти место для хранения значений добавляемого узла. Это такая небольшая, но крайне полезная функция, которая сокращает объем программного кода Insert_node и делает функцию Insert_node более выразительной и четкой.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
//------------------------------------------------------------------------------ // создание новой вершины, которую планируется добавить в дерево // key - ключевое значение создаваемой вершины // в качестве результата функция вернет указатель на созданный узел //------------------------------------------------------------------------------ Node* Create_node( const int key ) { Node* new_node = ( Node* )malloc( sizeof( Node ) ); new_node -> key = key; new_node -> left = new_node -> right = NULL; return new_node; } //------------------------------------------------------------------------------ |
В итоге с добавлением узла в «бинарку» мы разобрались! Написали $2$ программные функции: Insert_node и Create_node. Я привел пример лишь одного из вариантов реализации такого добавления
Пора двигаться дальше!
Добавить комментарий