Решил написать заметку-шпаргалку, в которой зафиксировать алгоритм нахождения общего предка ( вершины ) для двух заданных узлов ( вершин-потомков ) в двоичном дереве поиска.
Для анализа алгоритма мне потребуется некоторое двоичное дерево поиска, допустим, такое:
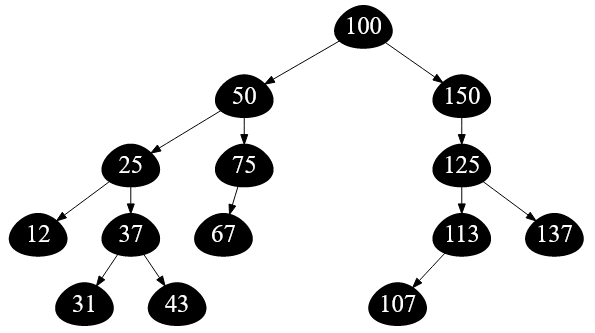
Рисунок — стандартное дерево поиска ( ключи — натуральные числа )
➡ Из постановки алгоритма следует, что для начала надо задать две вершины. Именно для этих вершин ( потомков ) я буду искать общего минимального предка.
Пусть первой вершиной-потомком будет узел двоичного дерева с ключом $12$:
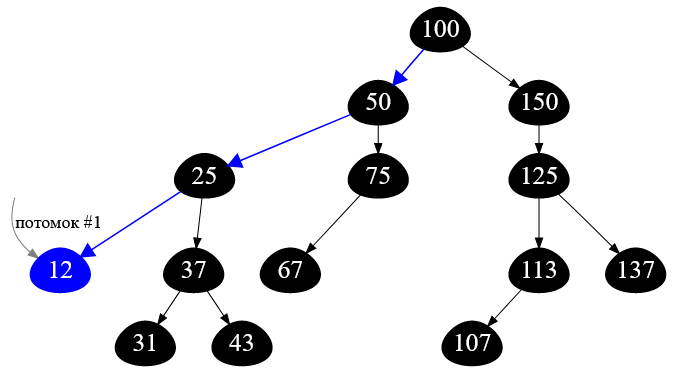
Рисунок — путь от корня до вершины с ключом $12$
Пусть второй вершиной-потомком будет узел двоичного дерева с ключом $67$:
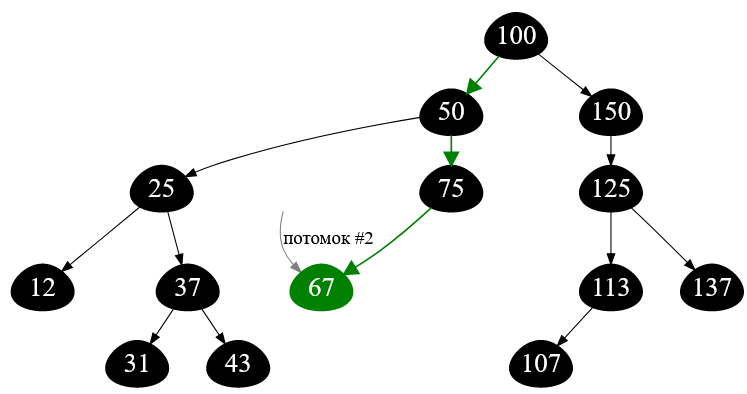
Рисунок — путь от корня до вершины с ключом $67$
Для заданных двух вершин с ключами $12$ и $67$ искомым минимальным предком будет элемент бинарного дерева с ключом $50$:
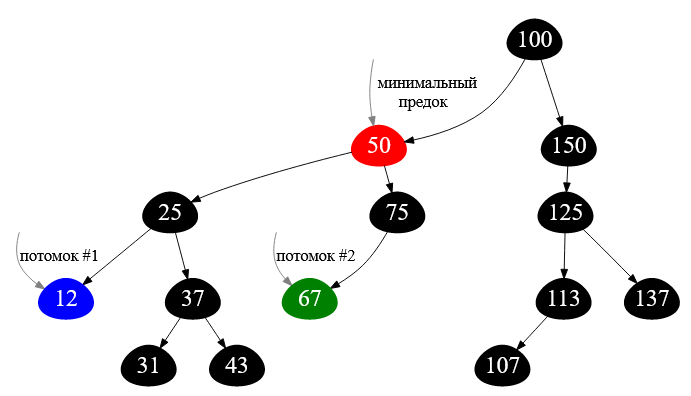
Рисунок — наименьший общий предок для вершин $12$ и $67$
А почему, собственно, вершина с ключом $50$ является наименьшим общим предком?
Наименьшим общим предком двух вершин $u$ и $v$ двоичного дерева поиска называется такая вершина $p$, которая лежит на пути от корневой вершины дерева и до вершины $u$, и до вершины $v$, при этом вершина $p$ максимально удалена от корня дерева.
| Ключ вершины | Путь от корня до вершины |
| $12$ | $100 -$ $50$ $- 25 — 12$ |
| $67$ | $100 -$ $50$ $- 75 — 67$ |
Сейчас я введу некоторые ограничения на входные данные для алгоритма поиска наименьшего общего предка:
| ➡ | Двоичное дерево поиска, в котором ищется наименьший общий предок, должно содержать заданные две вершины-потомка. То есть я не буду рассматривать случай, когда, например, одной из вершины физически нет в дереве. |
| ➡ | Путь до одной из заданной вершины-потомка не должен являться частью пути до другой заданной вершины-потомка. Это исключает случай, когда искомым минимальным общим предком будет один из заданных узлов-потомков. |
Поясню картинкой смысл второго ограничения:
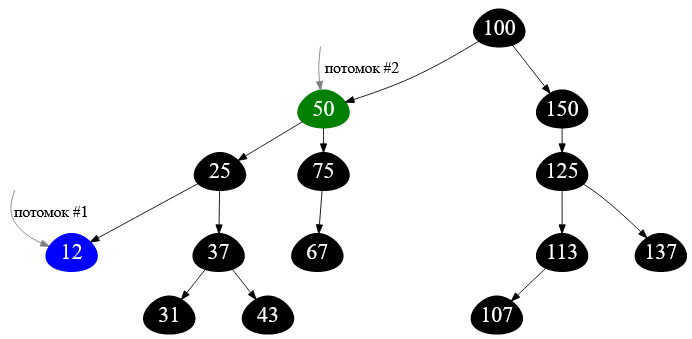
Рисунок — весь путь до вершины $50$ является частью пути до вершины $12$
➡ Если говорить неформально, то искомый минимальный общий предок должен быть «точкой перелома» пути между двумя заданными узлами-потомками. На рисунке выше это условие не выполняется.
Также в формулировке алгоритма встречается слово «минимальный». О чем речь?
Все дело в том, что у некоторых вершин бинарного дерева поиска есть несколько предков, стоящих на разных уровнях дерева. Есть понятие прямого предка и косвенных.
➡ Кстати, у корневой вершины нет ни одного предка, так как эта вершина сама является супер-родителем для всех вершин двоичного дерева.
Хочу показать картинку, на которой выделены цветом все предки ( прямой родитель красным, а косвенные — оранжевым ) для вершины с ключом $113$:
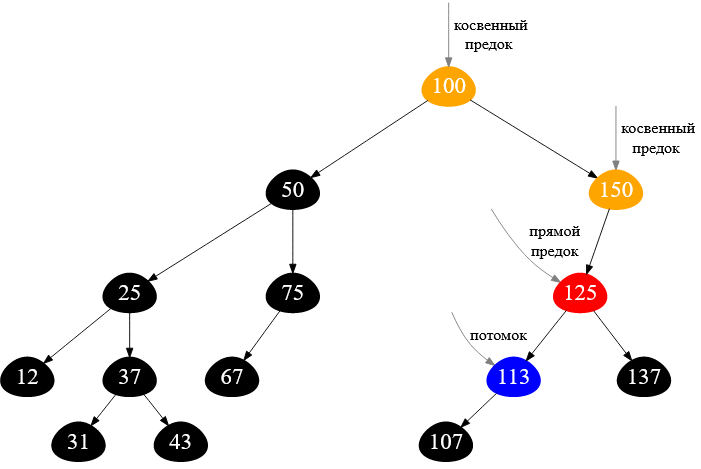
Рисунок — все родительские вершины для узла с ключом $113$
Минимальный предок — это вершина бинарного дерева поиска, расположенная наиболее близко к заданному узлу-потомку. Очевидно, что этот предок будет наиболее удален от корневого элемента дерева.
➡ Если в формулировке алгоритма опустить слово «минимальный«, то сразу появляются неоднозначности, так как количество общих предков двух узлов может быть больше одного! А наименьший общий родитель ( если он существует ) — всегда единственен.
💡 Переходим к основной идее алгоритма поиска наименьшего общего предка в двоичном дереве поиска.
На входе у меня есть построенное бинарное поисковое дерево ( root — указатель на корневой узел дерева ) и значения ключей двух вершин-потомков, для которых ищется минимальный родитель.
Думаю, что закодирую рекурсивную функцию ( напомню, что древовидные структуры крайне удобно обрабатывать рекурсивно ), которая будет «прокладывать путь» до любого из двух заданных потомков, но при этом на каждом уровне дерева проверять местоположение потомков относительного текущего узла.
➡ Как только узлы-потомки окажутся в разных поддеревьях относительно текущего узла, то делаю вывод, что искомый наименьший предок найден — текущая вершина дерева.
Вот моя реализация поиска минимального общего родителя в двоичном поисковом дереве на языке программирования «чистый» Си ( стандарт языка C89 ):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
//------------------------------------------------------------------------------ // подготовительная функция перед поиском наименьшего общего предка // в этой функции с клавиатуры вводятся значения ключей двух вершин-потомков // также внутри этой функции происходит вывод результата на экран пользователя //------------------------------------------------------------------------------ const void Prepare_least_common_ancestor( const Node* const root ) { const Node* min_ancestor; int vkey, ukey; printf( "\n\nВведите через пробел 2 целых числа ( ключи вершин, для которых ищется мин.предок ): " ); scanf( "%d %d%*c", &vkey, &ukey ); min_ancestor = Least_common_ancestor( root, vkey, ukey ); printf( "\nЗначение ключа наименьшего общего предка: %d", min_ancestor -> key ); } //------------------------------------------------------------------------------ // поиск минимального общего предка для заданных узлов-потомков ( v, u ) // node - указатель на текущую вершину двоичного дерева поиска // vkey - значение ключа первого заданного узла-потомка // ukey - значение ключа второго заданного узла-потомка // в качестве результата функция вернет указатель на наименьший общий предок //------------------------------------------------------------------------------ const Node* Least_common_ancestor( const Node* const node, const int vkey, const int ukey) { // это условие вернет ИСТИНУ, если заданные вершины-потомки лежат в разных поддеревьях // относительно узла node if ( ( vkey < node -> key ) != ( ukey < node -> key ) ) { return node; } // прокладываем путь до вершины v ( можно было и до u - разницы нет ) if ( vkey < node -> key ) { return Least_common_ancestor( node -> left, vkey, ukey ); } else { return Least_common_ancestor( node -> right, vkey, ukey ); } } //------------------------------------------------------------------------------ |
И, как обычно, рекурсивное решение компактно, наглядно и предельно строго.
И сейчас я протестирую работу функции Least_common_ancestor() на следующем бинарном дереве поиска:
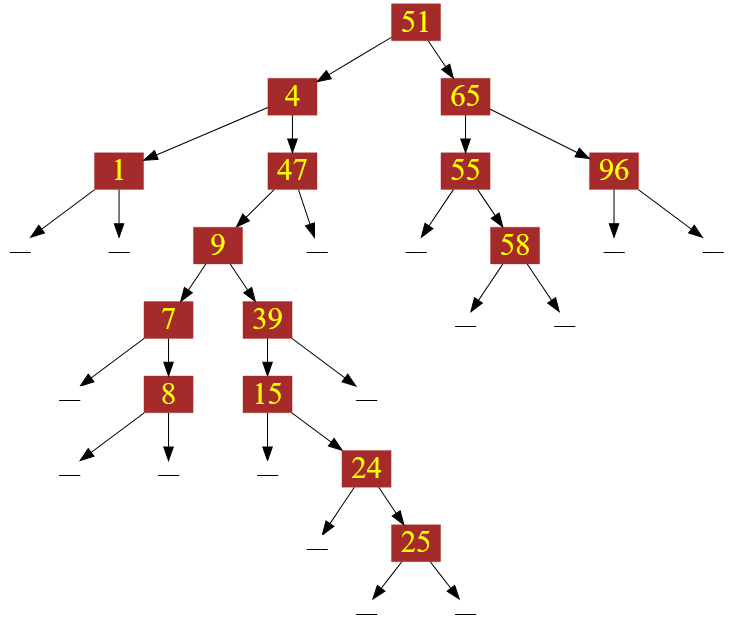
Рисунок — стандартное двоичное дерево поиска для тестирования
В итоге получаю следующие результаты:

Рисунок — тест #1

Рисунок — тест #2
💡 Добавлю несколько фраз про вычислительную сложность данного алгоритма ( в теории программирования его называют lca ).
Учитывая тот факт, что рассматриваемые двоичные деревья поиска не являются сбалансированными по высоте, можно сделать вывод, что худший случай будет $O( n )$, где $n$ — общее количество вершин дерева.
➡ Также не стоит забывать, что алгоритм, рассмотренный в этой статье-заметке, далеко не единственный алгоритм поиска общего наименьшего предка. Существуют более сложные и хитрые алгоритмы, имеющие гораздо лучшие показатели вычислительной сложности, чем $O( n )$. В текущем же алгоритме все по сути сводится к поиску одной из заданных вершин-потомка.
Пишите в комментариях, что непонятно в рамках рассмотренного алгоритма, а также случаи из вашей практики, когда вам пригодился поиск наименьшего предка в бинарном дереве поиска.
| ВНИМАНИЕ | Для заказа программы на двоичное дерево ( поиска ) пишите на мой электронный адрес proglabs@mail.ru |
Добавить комментарий